Soter library #
Soter is a cross-platform multipurpose cryptographic library that serves as a backbone for Themis. It provides a set of highly secure cryptographic primitives through a well-defined, consistent, and simple interface.
To name just a few things you can get with Soter (as the rabbit hole of its true capabilities runs much, much deeper):
- cryptographic primitives necessary for building robust secure solutions
- intuitive, well-defined interface for cryptographic functions
- compile-time support for interchangeable cryptography implementations
- object-oriented design
- portability utilities
Soter does not provide all the possible existing cryptoalgorithms. Instead, we tried to select the best ones for our cryptosystems (and future features) and provide a simple way of using them even for an inexperienced user. Also, we tried to provide the freedom in choosing the underlying cryptographic implementation for each of them.
The code is cleanly split into the generic part and the implementation- and/or platform-specific part, so porting the library to a different crypto implementation is very easy. Every function can be re-implemented using different cryptographic libraries. Appropriate source files are selected for compilation through compile-time switches. Thus, every instance of Soter library can be tweaked to support any platform-preferred implementation of the algorithms while still providing a consistent interface for its users.
We are currently using OpenSSL’s libcrypto by default,
but plan to replace it in the future releases.
Read more about cryptography providers for Themis.
Soter crypto stack #
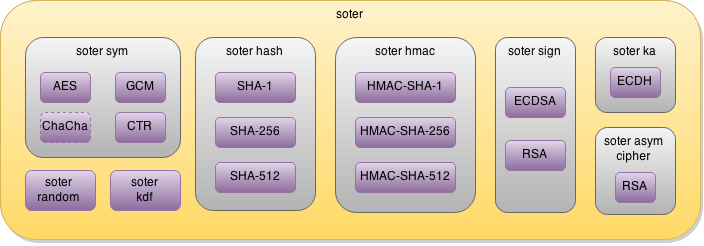
While selecting the necessary cryptographic building blocks for our solutions, we had the following concepts in mind:
-
All basic cryptographic operations should be supported: symmetric cryptography, key agreement, digital signatures, data integrity and authentication.
-
All algorithms we’re using should be open and well-established – such that underwent significant industry review(s).
-
All algorithms should use/support the latest “state-of-the-art” achievements and techniques in the field of data protection/information security.
-
All cryptographic modes of operation should be as transparent as possible for the user while imposing little additional overhead.
-
Combination of such primitives should allow information security protection with a high level of security.
Selected cryptographic algorithms #
Symmetric encryption #
Advanced Encryption Standard (AES) is the main algorithm we use for symmetric encryption. This algorithm is rather simple, fast, and proven to be secure. Also, many platforms currently have hardware support for AES, so our solutions can get additional performance improvements on such platforms.
We also consider using ChaCha as another future choice for our solutions.
Encryption modes
Galois/Counter Mode (GCM) is our main cryptographic mode of operation for AES. GCM is a relatively new concept in symmetric cryptography. It is a variant of “authenticated encryption”—a mode which combines information confidentiality, integrity, and authentication. When information is being decrypted its integrity and authenticity are verified simultaneously.
This is not only faster and more convenient but it is also generally considered to be more secure than applying encryption and message authentication code separately. Key management is also easier because a single key is used for both encryption and data authentication without compromising security.
Since GCM mode requires adding (storing, passing) additional message authentication code (MAC), the size of protected information increases. This behaviour may be undesirable or even unacceptable for some use cases. For such scenarios we use counter mode (CTR) instead.
The counter mode does not require the original information to be padded and has additional properties that allow implementations to parallel the computations of ciphertext. Although this mode does not provide information integrity and authentication functionality, it still ensures a high level of confidentiality while having less strict requirements for cryptographic parameters compared to other modes (like CBC).
Digital signatures #
Elliptic Curve Digital Signature Algorithm (ECDSA) is our main digital signature scheme. Elliptic curve-based cryptosystems usually provide higher security levels with smaller keys. Currently, there are no publicly known efficient algorithms for breaking elliptic curve keys. Since these keys are very small, they are also easier to generate and store. The overall computational load is reduced, too.
We also support RSA mainly to provide some level of compatibility with already established solutions. However, this is just a “back-up plan” option available to stay on the safe side.
Key agreement #
Elliptic Curve Diffie–Hellman (ECDH) is our key agreement scheme for the reasons similar to choosing ECDSA: elliptic curve-based cryptosystems are just better than their “plain” counterparts. Also, much of the elliptic curve implementation is reused (if the same or similar cryptographic parameters are used), so most of the code is shared between ECDH and ECDSA.
Diffie-Hellman and ECDH are susceptible to man-in-the-middle-attack (MitM), so we usually combine their usage with strong authentication in our solutions – ECDSA digital signatures – to mitigate such attacks.
Asymmetric encryption #
While Soter supports RSA asymmetric encryption, we recommend (and prefer using in our modules) the elliptic curve-based cryptosystems. However, there are no direct well-established asymmetric encryption schemes in the ECC-based domain. A simple combination of ECDSA+ECDH can be used to provide similar functionality in two steps:
-
Use peer’s public ECDH key and your own private ECDH key to compute a shared secret – which will be used to encrypt the message as in RSA encryption.
-
Send your own signed ECDH public key to the peer, enabling them to compute the same shared secret and decrypt the message.
This approach even has an advantage over RSA encryption: ECDH keys may be random and only used once. This provides perfect forward secrecy (PFS) to overall communication.
Data integrity and authentication #
The SHA family of algorithms is implemented for checking the data integrity in our solutions. These algorithms have been out for a while, and still no significant attacks on them are currently known. In our schemes, we use SHA-2 (SHA-256 or SHA-512).
For data authentication, we use GCM mode where applicable (usually combined with encryption). In other cases, we use hash-based message authentication code (HMAC). The security level of HMAC mostly depends on the security level of the underlying hash functions. It means that the security level in our implementation is high since we mostly use SHA-2. Every supported hash function can be used in HMAC as well.